文章地址:https://dl.acm.org/doi/10.1145/2588555.2610509
标题:Resolving Conflicts in Heterogeneous Data by Truth Discovery and Source Reliability Estimation
作者:Qi Li, Yaling Li, Jing Gao, Bo Zhao, Wei Fan, Jiawei Han
发表会议:SIGMOD 2014
- Introduction
- Methodology
- Problem Formulation
- CRH Framework
- Source Weight Assignment
- Truth Computation
- Discussions & Practical Issues
- Summary
- Experiments
- Experiment Setup
- Performance Measures
- Baseline Methods
- Experimental Results
- Real-world Data Sets
- Noisy Multi-source Simulations
- Efficiency
- Experiment Setup
- Conclusions
Abstract
很多应用中,个人可以从多个数据源获得对同一物体的描述信息。由于不同数据源对数据的描述不一定相同,冲突会产生。一个重要的问题是识别不同数据源中哪个数据是真实的(Truth)。简单的想法是我们可以信任可靠的数据源,但是我们并不知道哪个数据源可靠。同时,不同的数据类型也会给这一任务带来挑战。已有的冲突解决方法没有考虑到数据源的可靠性。在本文中,我们提出了一个优化框架将事实Truth和数据源作为两个未知变量去考虑,同时我们考虑多种数据类型。实验效果表明我们提出的框架效果很好。
Introduction
在大数据的背景下,不同的数据源对不同的物体可能会得到不同的观测结果。比如,一个客户的信息可能会出现在一个公司的不同的数据集中,病人的记录可能出现在不同的医院中等。
由于各种错误,比如设备采取数据精度,不同的数据源对于同一个实体可能会得到不同的观测结果。但是真实值只有一个,如何从有冲突的数据中得到 truth 当前面临挑战。即 It is critical to identify the most trustworthy answers from multiple sources ofconflicting information. 由于以下两个挑战,这个问题是很有意义的:
Challeng 1. Source Reliability
在数据集成中,从不同数据源中解决冲突已经被研究多年了。在这些方法中,对于categorical 数据一个常用的方法就是采用投票。但是当前的方法假定不同数据源的可信程度是一样的。因此,衡量source reliability非常重要。
Challeng 2. Heterogeneous
现实中的数据集往往包括了多种数据类型,比如医疗系统中可能暴扣年龄,身高,体重,地址等。因此,同时考虑到 categorical data, 连续数据等是有用的。
由于现实中的数据丢失,我们通常没有足够多的数据去衡量数据源的可靠性,所以我们需要提出一个统一的模型来进行对不同数据的估计。所以作者提供了一个 CRH 框架,叫 Conflict Resolution on Heterogeneous Data。总的来说有以下几个贡献点:
- 提出了一个统一的优化框架来解决含有不同类型数据的数据冲突问题。
- 在这个框架中,采用了不同的loss函数。
- 提出了一个分步优化的方法来解决这个优化问题。
- 在真实数据和生成的数据中去衡量有效性。
Methodology
Problem Formulation
在定义正式的问题之前,我们需要定义一些概念。
定义1. Object: 一个对象,一个对象有不同的属性。比如 Bob 是一个对象,有身高和所在城市两个属性。
定义2. Observation:一个数据源对于一个对象的观察值,比如某个数据源1 记录 Bob 身高是1.74m。
定义3. Entry:一个对象的一个属性,比如Bob 的身高是一个entry。 the truth of entry就是真实值,即Bob的真实身高。
有了这些定义之后,就可以定义系统的输入输出了,我们先来看系统输入部分。
定义4. 第 $k$ 个数据源观察到的物体 $i$ 的第 $m$ 个属性是 $v_{im}^{(k)}$。
定义5. 第 $k$ 个数据源对所有对象的观察结果记为 $\mathcal{X}^{(k)}$,因此从 $K$个数据源中,可以得到一个观察表,记为:$\{\mathcal{X}^{(1)}, \mathcal{X}^{(2)}, …, \mathcal{X}^{(K)}\}$
定义6. Truth Table,即真实结果。

比如上图给了一个例子,其中有五个object,三个数据源以及每个对象有两个属性。表1显示的是不同数据源的观察值,表2给出的是真实值以及不同方法估计出的结果。
为了解决 truth discovery的问题,本文定义了数据源权重。
定义7. 数据源权重用 $\mathcal{W}=\left\{w_{1}, w_{2}, \dots, w_{K}\right\}$ 表示。其含义为每个数据源的权重。
CRH Framework
我们可以这么认为,如果某个数据源提供的数据越接近于真实值,那么这个数据源就越可靠,因此数据源的带权值就相对来说越低。所以本文提出了一下一个优化框架,在本文中,这个公式称为公式1。
其中有两类函数需要进行考虑:
- Loss Function. $d_m$ 记为衡量第 $m$ 个属性的loss。这个函数的功能就是用来表示真实值和观测值的距离。
- Regularization function. $\delta(\mathcal{W})$ 用来表示数据源权重的分布,也是数学上归一化要求。
这两类函数不是一层不变的,而是可以根据数据特征灵活选择。同时,事实 $\mathcal{X}^{(*)}$ 和 $\mathcal{W}$ 应当同时进行学习,直到收敛。总共分为两步进行:
- Step.1 数据源权重更新。首先根据真实值和观测值的不同去更新每个数据源的权重,利用下面的公式2:
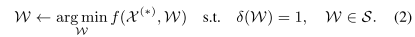
- Step.2 事实更新,根据每个用户的值和权重去更新事实 $\mathcal{X}^{(*)}$,利用下面的公式3:
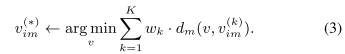
给了这两步之后,CRH算法的框架如下图所示:

Source Weigh Assignment
作者在文中给出了这样的归一化方程:
给定上式之后,作者有了定理1.
定理1. 假定 truth 固定不变,那么以 $\delta(\mathcal{W})$ 为限制的优化问题是凸的,最优解由以下方程给出
定理1的证明过程就不在此仔细展开了,感兴趣可以参考原文。上述定理表明,数据源的权重与数据源和truth之间的差距决定。上述公式可以将一个0-1的范围映射到0到正无穷,即数据源的观测值和真实值越接近,那么数据源的权重就会越高。
Truth Computation
公式3的truth计算依赖于数据类型和loss函数,这里首先考虑了categorical data和continuous data。首先来看看categorical data。最常见的loss是0-1loss,定义如下:
给定这个之后,我们就有下面的定理:
定理2. 假定权重固定,基于0-1loss,公式3的优化结果为:
其中,$\mathbb{1}(x,y)=1$ 如果 $x=y$。
定理2的证明这里就不介绍了。
当truth只有一个值的时候,我们可以采用0-1loss,因为观测值要么和truth一样,要么不一样。那么当 truth $v_{im}^{(*)}$ 有多个值的时候怎么办呢,假如第 $m$ 个属性有 $L_m$ 个可能的值,并且 $v_{im}^{(k)}$的值是第 $l$ 个值,那么建立这样一个向量:
然后我们用squared loss去计算,为:
对于这样一类,类似于定理2,我们有定理3:
假设权重固定,采用上述的loss函数,最优的 $I_{im}^{(*)}$ (表示truth的分布)为:
上述过程是针对categorical data 的处理,对于连续数据,一种常用的loss是 normalized square loss,定义为:
类似于定理2和定理3,定理4给出的最优解为:
上述loss中,异常值会带来比较大的影响,有时候我们也可以采用normalized absolute deviation作为loss,定义为:
然后定理5说,基于这个loss,truth应该为带权重的中位数。
Discussions & Practical Issues
这里首先讲了几个在实际应用当中比较重要的问题,包括 Initialization, Convergence, Normalization和Missing values。然后用一个案例展示我们提出的算法,最后分析了时间复杂度。
Initialization 在优化的过程中,首先需要给truth随机化一个值,然后进入迭代。我们发现,可以将已有的基于投票/均值的结果用于对truth初始化。我们发现这个方法效果还不错。事实上,初始化的参数选取并不会影响最终的结果。
Convexity and Convergence 算法的convexity取决于loss函数和归一化函数。一个图的loss函数家族是Bregman divergence,其中包括了一系列loss函数,包括squared loss,logistic loss,Itakura-Saito距离,squared欧几里得距离,manhalanobis距离,KL散度和generalized I-散度。我们证明CRH框架的convergence如下。
定理6: 当方程4作为归一化条件,方程16或19作为loss函数,我们可以保证CRH的convergence。
Normalization 这里是说当对于不同的属性采用不同的 loss 的时候,不同属性的loss的大小是不一样的,为了解决这个问题,每个loss需要归一化,这样每个loss的范围就一样了。
Missing Values 为了简化问题,本文假定所有的数据源有着对所有物体的所有属性的观察值。当数据丢失,即数据源只有这对一部分物体的一部分属性有观测值的时候,我们可以normalize the overall distance of each source by the number of observations。(这句话我也没get到什么意思)。
Running Example 作者给了一个running example 表明了迭代过程。可以照着算一下。
Summary
讲了一下本文的贡献。CRH模型统一了不同的数据类型。提出的最优化模型考虑了数据源的权重,比目前不关注数据源的方法更有优点。
Experiments
开始讲实验了,首先讲了实验的配置,然后呈现实验结果。
Experiment Setup
这部分讲如何衡量实验效果以及对比哪些方法。
Performance Measures
如何衡量估计效果呢,分为以下两个方面:
- Error Rate: 对于categorical 数据,我们采用错误率,就是估计错了的频率。
- MNAD: 对于连续数据,采用MNAD,即Mean Normalized Absolute Distance。
对于上面两个衡量方法,数据越小, 估计的就越接近truth,方法的表现就更好。(连续数据这样很正常,为什么error rate也是这样?)
Baseline Methods
CRH中,对于categorical data,默认采用weighted voting(文中的公式13,即0-1loss哪个迭代方程:$v_{i m}^{(*)} \leftarrow \underset{v}{\arg \max } \sum_{k=1}^{K} w_{k} \cdot \mathbb{1}\left(v, v_{i m}^{(k)}\right)$),对于连续数据,采用weighted mean,即文中的公式23。对比的方法分为以下三类:
Conflict Resolution Methods Applied on Continuous Data Only:
- Mean:采用均值作为truth。
- Median:采用中位数作为truth。
- GTM[23]:Gaussian Truth Model,是一个Bayesian probabilistic 方法。
Conflict Resolution Methods Applied on Categorical Data Only:
- Voting:采用投票方法,出现次数最多的作为truth。
Conflict Resolution Methods by Truth Discovery:
- Investment[18]
- PooledInvestment[18]
- 2-Estimates[12]
- 3-Estimates[12]
- TruthFinder[22]
- AccuSim[9]
由于这些方法之前也没看过,对比的方法就先留空了,可能也不更新了,如果下次需要做这方面的东西,再来了解。
Experimental Results
实验篇幅较长,仅仅选取了一些做呈现。
Real-world Data Sets
文中采用了这几个数据集:
- Weather Forecast Data Set:
- Stock Data Set:
- Flight Data Set:
这几个数据集的统计特征如下表所示:
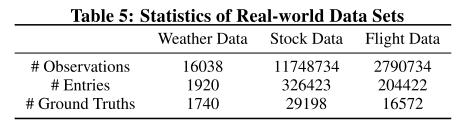
表6给了一个总的实验结果,可以看出作者的方法最好。
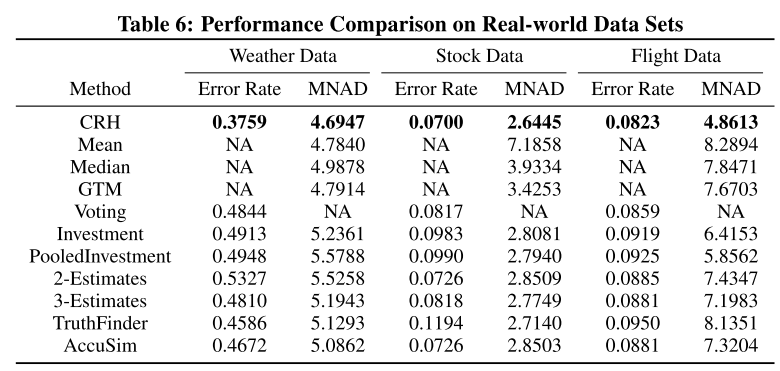
Noisy Multi-source Simulations
这里作者生成了两个数据集,然后用做测试,生成的数据集的统计特征如下:

同样的,实验结果如表9所示:

Efficiency
在效率这方面,作者从两个角度考虑实验效果。
首先是收敛程度,图5展示了随着迭代过程的进行,目标值的变化:

其次是程序的运行时间,结果如表11所示。实验的配置也没有细看。

本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


